これもアマチュア無線国家試験の問題です。
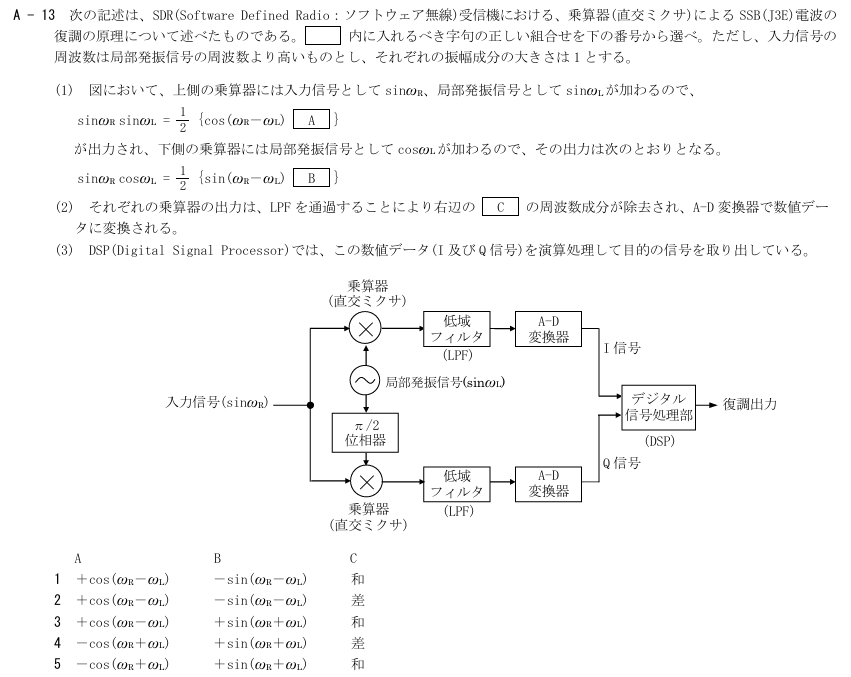
なんとなく難しそうに見えますが、実際は簡単で図をみたら直ぐに答えが分かるのです。これは最後に説明するとして、一応計算してみたいと思います。
\(
先ずは、加法定理からです。\\
\begin{align}
\sin(\alpha+\beta) &=\sin\alpha \cos\beta + \cos\alpha \sin\beta \tag{1}\\
\sin(\alpha-\beta) &=\sin\alpha \cos\beta \,- \cos\alpha \sin\beta \tag{2}\\
\cos(\alpha+\beta) &=\cos\alpha \cos\beta \,- \sin\alpha \sin\beta \tag{3}\\
\cos(\alpha-\beta) &=\cos\alpha \cos\beta + \sin\alpha \sin\beta \tag{4}\\
\end{align}\\
\)
\(
(1) + (2) = \sin(\alpha+\beta) + \sin(\alpha-\beta) = 2\sin\alpha \cos\beta\\
\)
\(
\begin{align}
これより \sin\alpha \cos\beta = \frac{1}{2}\{\sin(\alpha+\beta) + \sin(\alpha -\beta)\} \tag{5}\\
\end{align}
\)
\(
(4) – (3) = \cos(\alpha -\beta) – \cos(\alpha+\beta) = 2\sin\alpha \sin\beta\\
\)
\(
\begin{align}
これより \sin\alpha \sin\beta = \frac{1}{2}\{\cos(\alpha-\beta) – \cos(\alpha+\beta)\} \tag{6}\\
\end{align}
\)
\(
\alpha = \omega_R, \beta = \omega_Lとすると\\
\)\(
Aは (6)から \sin\omega_R\sin\omega_L = \frac{1}{2}\{\cos(\omega_R-\omega_L) – \cos(\omega_R+\omega_L)\}
\)
\(
Bは (5)から \sin\omega_R \cos\omega_L = \frac{1}{2}\{\sin(\omega_R-\omega_L) + \sin(\omega_R+\omega_L)\}
\)
\(
LPF(ローパスフィルタ)を通すから、高い周波数である「和」の成分、\\
\cos(\omega_R+\omega_L)と\sin(\omega_R+\omega_L)は除去される。
\)
まぁ、計算しなくても…
乗算器(ミクサ)を通すと、二つの入力の周波数の和と差の周波数成分が得られます。
問題には、上側下側のどちらにも「差の周波数成分」が書かれているので、空欄に入るのは「和の周波数成分」になります。
回答の中で両方とも「和の周波数成分」なのは、４と５です。
そして、LPF(ローパスフィルタ)で除去できるのは周波数が高い成分である「和の周波数成分」になります。よって正解は5です。サービス問題だったかも知れませんね。
SDRで大切なのは、I,Q信号をどう処理するかかもね…