先日のアマチュア無線の国家試験で振幅変調AM(A3E)に関する問題が出ていましたね。
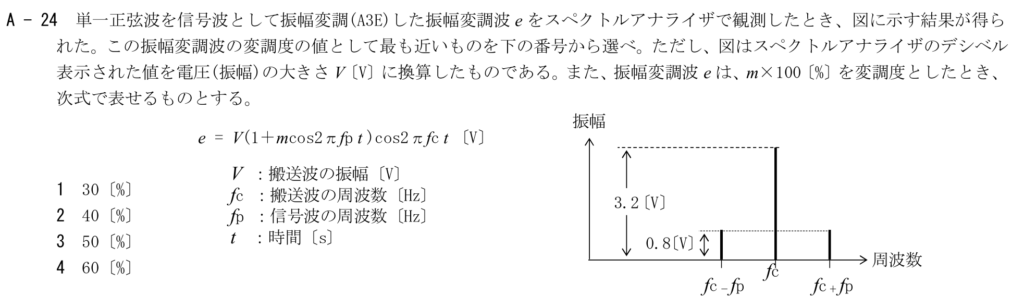
公式をおぼえていれば簡単なのですが、今回はこれを解いてみたいと思います。
\(e = V(1+m\cos 2\pi f_p t)\cos2\pi f_c t\)
\(ここで、表記を簡単にするために 2\pi f_p = \omega_p, 2\pi f_c = \omega_c とおくと\)
\(
\begin{align}
e &= V(1+m\cos\omega_p t)\cos\omega_c t \\
&= V(\cos\omega_ct+m\cos\omega_pt\cos\omega_ct) \tag{a}\\
&となります。
\end{align}
\)
\(高校の時に習った加法定理を思い出すと、\\
\begin{align}
\cos(\alpha + \beta) &= \cos \alpha \cos \beta – \sin \alpha \sin \beta \tag{1}\\
\cos(\alpha – \beta) &= \cos \alpha \cos \beta + \sin \alpha \sin \beta \tag{2}
\end{align}
\)
\(
(1) + (2) = \cos(\alpha + \beta) + \cos(\alpha – \beta) = 2\cos \alpha \cos \beta ですから,\\
\cos \alpha \cos \beta = \frac{1}{2}\{\cos(\alpha + \beta) + \cos(\alpha – \beta)\}に置き換えることができます。
\)
\(
\alpha = \omega_ct, \beta = \omega_pt とすると、
(a)の第二項の\cos\omega_pt\cos\omega_ct部分を置き換えて,\\
m\cos\omega_pt\cos\omega_ct =\frac{m}{2}\{\cos(\omega_c + \omega_p)t + \cos(\omega_c -\omega_p)t\}となります。\\
(a)に戻して、\\
V\cos\omega_ct+\frac{Vm}{2}\{\cos(\omega_c + \omega_p)t + \cos(\omega_c -\omega_p)t\}\\
これがA3Eを周波数成分に分解した式です。
\)
\(折角なのでf_c,f_pに戻しましょうか…\\
V\cos 2\pi f_ct +\frac{Vm}{2}\{\cos2\pi(f_c + f_p)t + \cos2\pi(f_c -f_p)t\} \\
\)
\(
\begin{align}
&V\cos2\pi f_ct&が搬送波(キャリア)\\
&\frac{Vm}{2}\cos2\pi(f_c + f_p)t &が上側波帯(USB) \\
&\frac{Vm}{2}\cos2\pi(f_c – f_p)t &が下側波帯(LSB)\\
&をあらわしています。
\end{align} \\
側波帯に周波数は、搬送波の周波数f_cに対して信号波の周波数f_pだけ\\上、下にシフトしていることが分かりますね。\\
そして、搬送波の振幅をV、変調度をmとすれば、\\側波帯の振幅は両側とも\frac{Vm}{2}となることも分かります。
\)
\( 設問に戻って\\
V = 3.2[V] のとき \frac{Vm}{2} = 0.8[V] となる mを求めればよいことになります。\\
\frac{3.2m}{2} = 0.8 から m = \frac{0.8 \cdot2}{3.2} = \frac{1.6}{3.2} = 0.5\\
つまり、変調度は50\%です。
\)
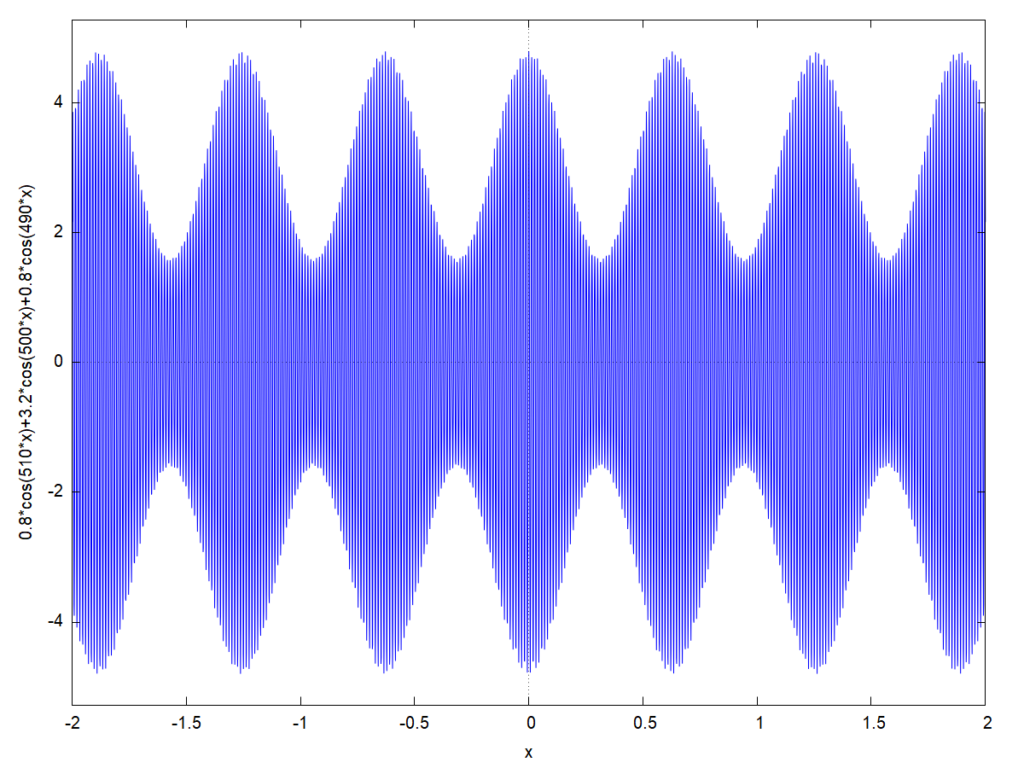
この時のA3E信号の波形は、こんな感じでしょう。
公式を覚えていなくても式が与えられているので加法定理さえ知っていれば簡単に求められますね。
加法定理の覚え方は、「咲いたコスモス コスモス咲いた、コスモスコスモス 咲いた咲いた」でしたね。思い出しましたか(笑)